मैं इनपुट I1, i2, और i3 के लिए मानों (0 या 1) के नीचे दिखाए गए आर्टिकियल न्यूरॉन के लिए निर्धारित करने की कोशिश कर रहा हूं जिसके लिए यह आग लगेगा (i0 पूर्वाग्रह वजन के लिए इनपुट है और हमेशा होगा -1)।कैसे निर्धारित किया जाए कि कृत्रिम न्यूरॉन किस मूल्य पर आग लगाएगा?
वजन
W0 = 1.5
W1 = -1
डब्ल्यू 2 = 1 हैं, और डब्ल्यू 3 = 2.
सक्रियण समारोह नीचे दी गई छवि में दिखाया गया मान लें।
कृपया अपने उत्तर,
मैरी जे
पी एस स्पष्ट रूप में मैं कुछ उदाहरण किया है और अभी भी मैं पूरी तरह से सिद्धांत :(
बहुत धन्यवाद समझ नहीं पा रहा हूँ। छवि नीचे:
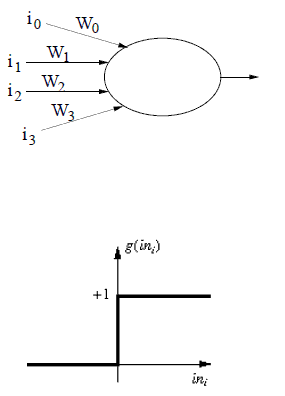
धन्यवाद gnovice, मुझे आश्चर्य है कि क्या आप मेरे दूसरे प्रश्न का उत्तर दे सकते हैं? अगर मैं अपने उदाहरण के लिए http://en.wikipedia.org/wiki/Artificial_neuron छद्म कोड एल्गोरिदम लागू करता हूं तो परिणाम आपके उत्तर के समान होगा? –
@mary: हां, वह छद्म कोड दिखाता है कि आप आउटपुट के मूल्य की गणना कैसे करेंगे (0 के थ्रेसहोल्ड मान के साथ)। यह अनिवार्य रूप से ऊपर दिए गए सूत्र का उपयोग करता है: यदि सूत्र सत्य का मूल्यांकन करता है (यानी बाएं तरफ भारित इनपुट का योग थ्रेसहोल्ड से अधिक है) तो न्यूरॉन से एक गैर-शून्य आउटपुट होता है। एकमात्र मुद्दा आपको ध्यान रखना होगा कि क्या ">" या "> =" का उपयोग किया जाना चाहिए (यानी यदि भारित इनपुट के लिए 0 योग 0 या 1 आउटपुट उत्पन्न करता है)। – gnovice
आपके अतिरिक्त स्पष्टीकरण, gnovice के लिए धन्यवाद। मैं इसके बारे में निश्चित नहीं था। आपके उत्तर के लिए बहुत धन्यवाद! –